作为流行病学调查方法的改进或替代,不妨借助外生的截断或删失机制。对于COVID-19,Backer等(2020)和Linton等(2020)都使用了在武汉外确诊的病例信息,利用区间删失似然方法来估计COVID-19潜伏期。在他们的研究中,从离开病源地到确诊的时间是一个被删失的区间,通过拟合伽马分布、对数正态分布或威布尔分布的潜伏期的截断区间,可以估计出潜伏期的分布。但是,由于偏性样本的问题,这种方法会得到有偏的估计。Qin等(2020)首次提出用更新过程的理论以克服偏性样本的问题得到了更好的潜伏期分布的估计。但拟合的是连续的时间分布,而实际上,每日报告确诊病例数是区间删失的,因为只能报告一天内的总新增确诊数量而不是在具体那个时刻发病。
一般来说,再生时间是从传染链上两个连续病例的发病时间差——即序列间隔来估计的,避免用到被感染的时间。这是因为,获得一串传染链上连续病例的感染时间是很困难的,而产生症状的时间相对容易获得。然而,用序列间隔代替再生时间可能会引起偏倚,特别是如果疾病在潜伏期内也有传染性,再生时间分布的方差可能会被高估。其结果是,基于再生时间计算的量是有偏的,例如,反映疾病传染能力的基本再生数会被低估。注意到COVID-19恰恰是潜伏期有传染性的,因此仅基于观测到的序列间隔来估计再生时间是不相合的。
为了克服前面提到的问题,周晓华团队借助于更新过程的理论,考察被某删失事件(离开武汉)截断的潜伏期。把潜伏期(从感染到产生症状)看作发生间隔时间(inter-arrival),离开武汉的感染者居民潜伏期被离开武汉这一事件所截断,再考虑到部分居民可能在离开武汉时(机场、火车站等场所)发生交叉感染,因而可以把离开武汉到产生症状的时间看作是区间删失的前进时间(截断事件到产生症状,forward time)与发生间隔时间(感染到产生症状)这二者的混合,同时考虑了由报告时间引起的区间删失问题。
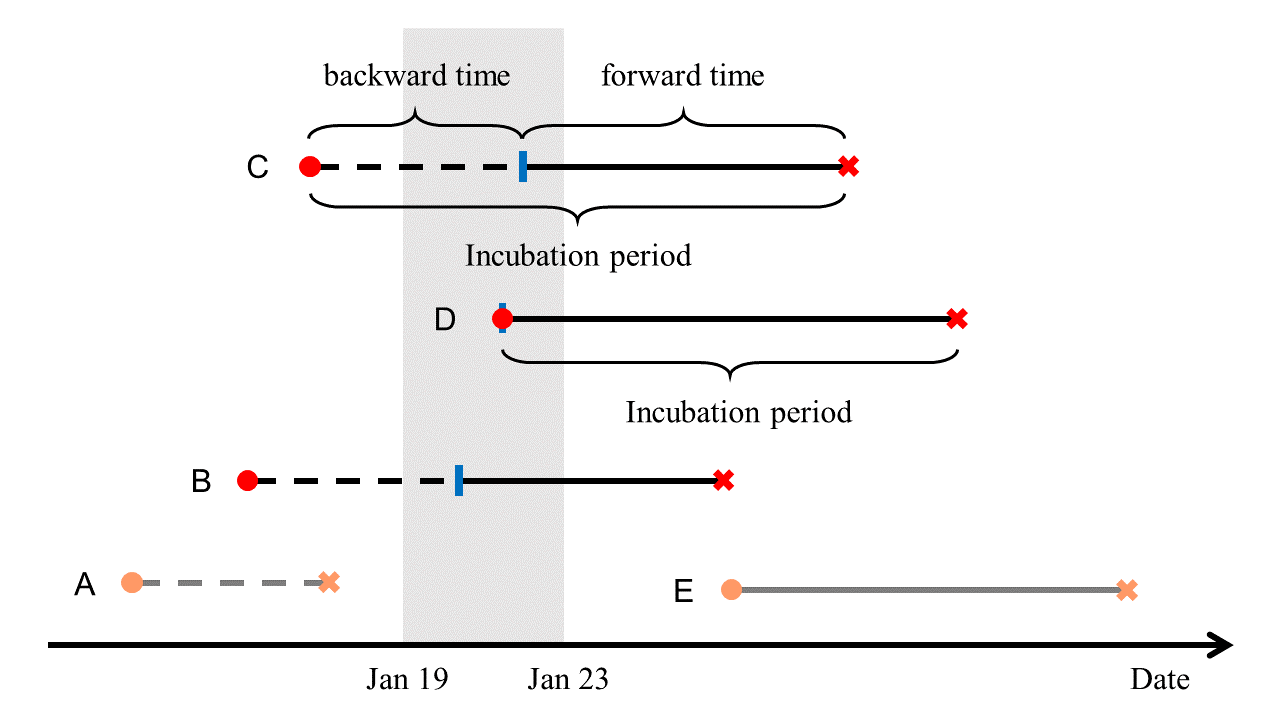
图:潜伏期、后退时间、前进时间。黑色线条表示纳入研究队列的人群,灰色线条表示未纳入研究队列的人群;实线表示观测到的,虚线表示未观测到的时间段。红色圆:感染时间;红色叉:产生症状时间;蓝色柱:离开武汉时间。
假设潜伏期服从伽马分布、威布尔分布或对数正态分布,观测队列为离开武汉后发病的人群,队列中在离开武汉当天感染的概率(混合概率)为π。在适当的条件下,作者证明了潜伏期分布参数、混合概率的可识别性的数学性质,并证明了这些参数估计量的大样本性质(服从渐进正态分布或截断正态分布)。对于混合概率π的假设检验问题,可以利用似然比检验给出。
和传统的流行病学调查相比,研究团队提出的方法可以减少回忆偏倚,增大可用样本量,有效利用删失信息,为新传染病流行的潜伏期估计提供了一种分析框架,其优势在传染病并爆发初期尤为明显。另外,基于潜伏期和观测到的序列间隔,在适当的假设下,通过反卷积运算,对潜伏期有传染性的疾病提出了再生时间的一个非参数的相合估计。
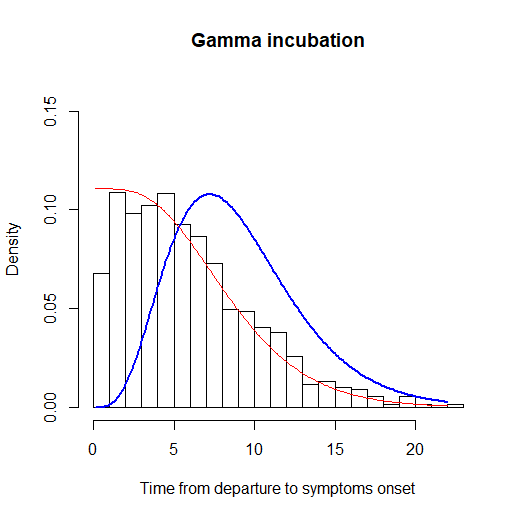

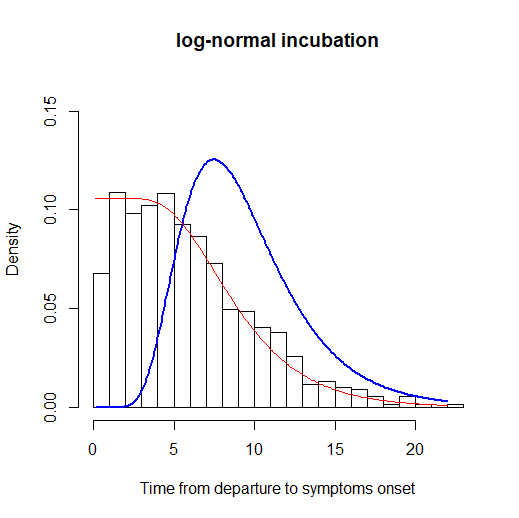
图:潜伏期分布的估计。红线表示前进时间的拟合,蓝线表示潜伏期分布的拟合

图:再生时间分布的估计。柱状图是序列间隔数据,黑线是序列间隔的非参数拟合,红线是再生时间分布的估计
国际生物统计学会出版的flagship杂志《Biometrics》强调统计和数学在生物科学中的作用。其目标是通过报道统计和数学方法的发展和应用,促进和扩大这些方法在生物科学主要学科中的应用。大多数生物统计学文章的核心是科学应用、确定科学或政策目标、激励方法的发展并展示新方法的操作。
本文的第一作者为数学科学学院博士生邓宇昊,第二作者为北京国际数学研究中心博士后尤翀,第三、第四作者分别为华东师范大学统计学院刘玉坤教授和美国国立卫生研究院生物统计研究所秦静数理统计学家,统计科学中心、北京国际数学研究中心、生物统计系的周晓华教授为本文通讯作者。本研究获国家自然科学基金(82041023, 11771144, 11971300, 11871287)、国家自然科学基金重点项目(71931004)、浙江大学新型冠状病毒肺炎应急科研专项资金、上海市人才发展资金、111计划(B14019)、中央高校基本科研业务费专项资金资助。

